Matrix Addition

In order to use the Kalman Filter equations, you will need to do matrix addition.

For example, the equation for calculating the error covariance matrix after the prediction step includes matrix addition:

\mathbf{P_{k|k-1}} = \mathbf{F_{k}} \mathbf{P_{k-1|k-1}} \mathbf{F_{k}^T} + \mathbf{Q_{k}}

or, using our simplified notation:

\mathbf{P}' = \mathbf{F} \mathbf{P} \mathbf{F^T} + \mathbf{Q}

Matrix Addition General Formula

As a reminder, this is the general formula for carrying out matrix addition:

\mathbf{A} + \mathbf{B} = \begin{bmatrix}a_{11} & a_{12} & \ldots & a_{1n}\\ a_{21} & a_{22} & \ldots &a_{2n} \\\vdots & \vdots & \ddots & \vdots \\a_{m1} & a_{m2} & \ldots & a_{mn}\end{bmatrix} + \begin{bmatrix}b_{11} & b_{12} & \ldots & b_{1n}\\ b_{21} & b_{22} & \ldots &b_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ b_{m1} & b_{m2} & \ldots & b_{mn}\end{bmatrix}

= \begin{bmatrix}a_{11}+b_{11} & a_{12}+b_{12} & \ldots & a_{1n}+b_{1n} \\ a_{21}+b_{21} & a_{22}+b_{22} & \ldots & a_{2n}+b_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1}+b_{m1} & a_{m2}+b_{m2} & \ldots & a_{mn}+b_{mn}\end{bmatrix}

The first element of matrix A is added to the first element of matrix B. The second element gets added to the second element, etc.

Matrix Addition Concrete Example

Here is a concrete example of matrix addition:

\mathbf{A} + \mathbf{B} =\begin{bmatrix}17&25&6&2&16\\6&1&97&4&22\\80&8&54&15&65\\11&25&68&9&2\end{bmatrix}+\begin{bmatrix}3&14&1&7&42\\32&11&2&4&18\\19&81&4&8&5\\27&2&3&6&7\end{bmatrix} = \begin{bmatrix}20&39&7&9&58\\38&12&99&8&40\\99&89&58&23&70\\38&27&71&15&9\end{bmatrix}

The graphic below shows how to calculate the sum. You take an element in matrix A and then add the matching element in matrix B that has the same position.

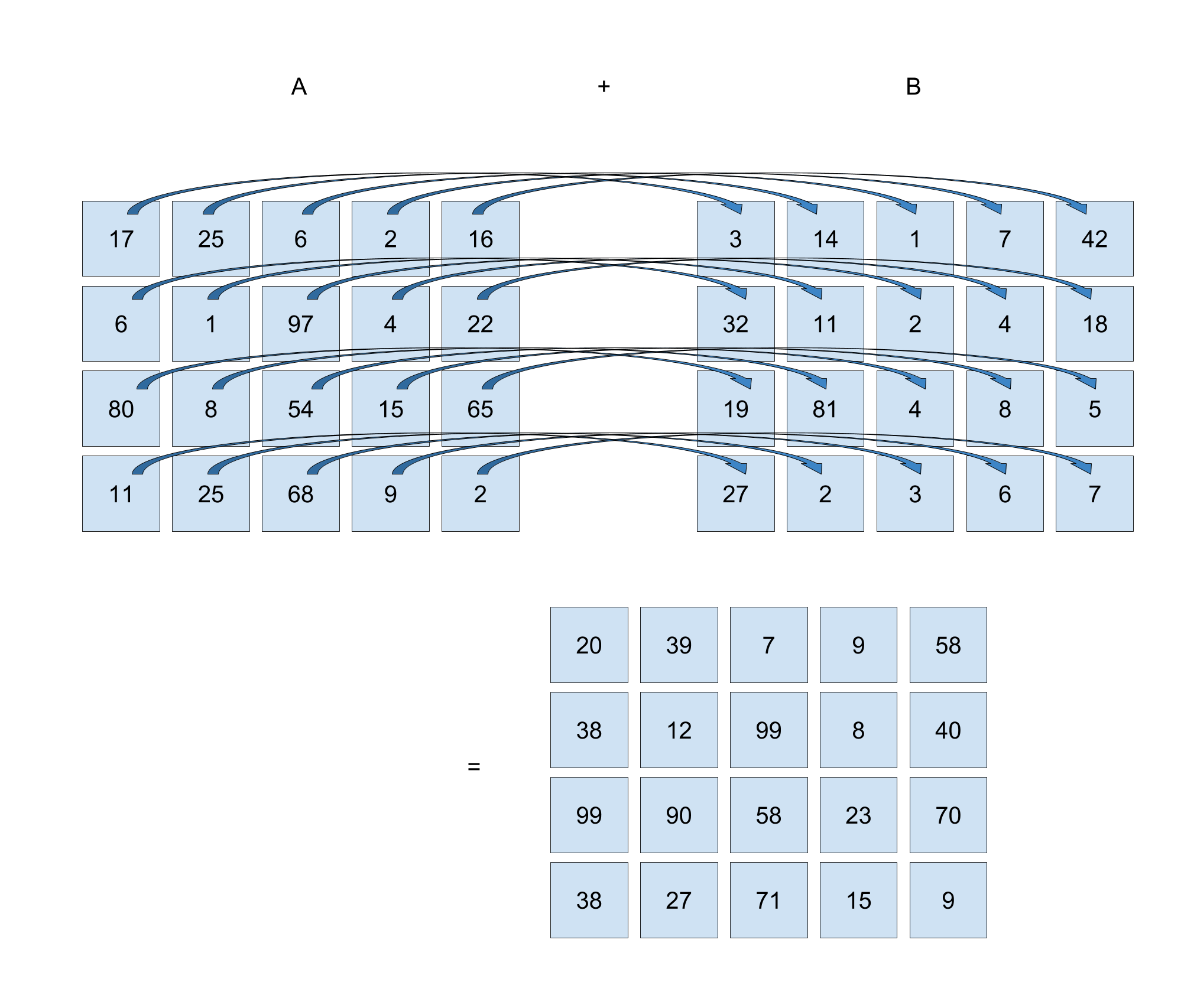
The top left element in matrix A is 17 and the top left element in matrix B is 3. The sum is 20, so the top left element of the resulting matrix is 20.

Here is another example: The second row third column A value is 97. The second row third column B value is 2. The sum is 99, so the second row third column resulting matrix has the value 99.

Characteristics of Matrix Addition

You will notice an important characteristic about matrix addition: the size of matrix A and matrix B need to be the same; in other words, they need the same number of rows and the same number of columns. If you go back to the Kalman Filter prediction equation shown at the top of the page, \mathbf{P_{k|k-1}} = \mathbf{F_{k}} \mathbf{P_{k-1|k-1}} \mathbf{F_{k}^T} + \mathbf{Q_{k}},

this means that the matrix \mathbf{Q_{k}} must be the same size as the matrix that results from multiplying \mathbf{F_{k}} \mathbf{P_{k-1|k-1}} \mathbf{F_{k}^T} .

Furthermore, the sum of two matrices will have the same size as well. So \mathbf{P_{k|k-1}} \text{as well as } \mathbf{Q_{k}} must have the same number of rows and columns.

Matrix Subtraction

To subtract two matrices, the same rules apply. To find \mathbf{A} - \mathbf{B}, you would subtract an element from B from its corresponding element in A.

Coding Matrix Addition

Matrix addition involves adding elements from the same position. So for S = matrix A + matrix B, you would need to do operations like these:

S[0][0] = A[0][0] + B[0][0]
S[0][1] = A[0][1] + B[0][1]
S[0][2] = A[0][2] + B[0][2]
S[0][3] = A[0][3] + B[0][3]
.... etc

S[1][0] = A[1][0] + B[1][0]
S[1][1] = A[1][1] + B[1][1]
...etc.

However, this code isn't very efficient for a number of reasons. You would have to write a line of code for every element in the matrix. If a matrix had 5 rows and 4 columns, you would need to write 20 lines of code. Another problem is that you won't always know beforehand how large your matrices will be. Your code might need to accommodate summing 5x4 matrices. But then your might also need to sum 10x2 matrices and any number of other configurations.

This is a perfect place to use nested for loops.

Using For Loops to Code Matrix Addition

In the previous exercises, you wrote code to do scalar multiplication. You also wrote a function that prints out a matrix.

The code for matrix addition is very similar. So try to do it on your own in the IPython notebook exercises on the next page.